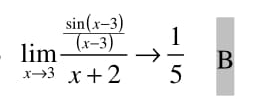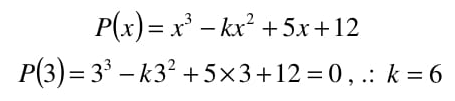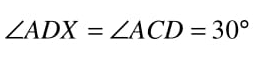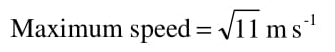2015 Mathematics HSC 3 Unit
Due to copyright restriction, we are not able to show the exam paper or questions on this website. As the answers, solutions and videos are our own work, these are all accessible on this page. Please use the following links to get a copy of the exam paper:
Exam Paper: click here Marking Guidelines: click here Notes from Marking Centre: click here
For all questions, see exam paper
1)
a
A
Question ID: 100130010010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130010010
Submit Yours! Copy Question ID and
click hereVideo by:
d
2)
a
C
Question ID: 100130020010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130020010
Submit Yours! Copy Question ID and
click hereVideo by:
d
3)
a
B
Question ID: 100130030010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130030010
Submit Yours! Copy Question ID and
click hereVideo by:
d
4)
a
C
Question ID: 100130040010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
Choose $8$ students from $12$ so $^{12}C_8$
Choose $1$ student from $4$ so $^{4}C_1$
Both events happening so AND event so multiply $^{12}C_8$$\times ^4C_1$
Question ID: 100130040010
Submit Yours! Copy Question ID and click here
Solution by: ada
Question ID: 100130040010
Submit Yours! Copy Question ID and
click hereVideo by:
d
5)
a
A
Question ID: 100130050010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130050010
Submit Yours! Copy Question ID and
click hereVideo by:
d
6)
a
D
Question ID: 100130060010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130060010
Submit Yours! Copy Question ID and
click hereVideo by:
d
7)
a
B
Question ID: 100130070010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130070010
Submit Yours! Copy Question ID and
click hereVideo by:
d
8)
a
B
Question ID: 100130080010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130080010
Submit Yours! Copy Question ID and
click hereVideo by:
d
9)
a
D
Question ID: 100130090010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130090010
Submit Yours! Copy Question ID and
click hereVideo by:
d
10)
a
C
Question ID: 100130100010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130100010
Submit Yours! Copy Question ID and
click hereVideo by:
d
11a)
a
$\frac12x-\frac14\sin2x+c$
Question ID: 100130110010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110010
Submit Yours! Copy Question ID and
click hereVideo by:
d
11b)
a
$\theta=\frac{\pi}{4}$ or $\theta=45^\circ$
Question ID: 100130110020
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110020
Submit Yours! Copy Question ID and
click hereVideo by:
d
11c)
a
$-3 < x\le 1$
Question ID: 100130110030
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110030
Submit Yours! Copy Question ID and
click hereVideo by:
d
11d)
a
$13\left(x+\tan^{-1}\left(\frac{12}{5}\right)\right)$
Question ID: 100130110040
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110040
Submit Yours! Copy Question ID and
click hereVideo by:
d
11e)
a
$\frac14\left(\ln3+\frac23\right)$
Question ID: 100130110050
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110050
Submit Yours! Copy Question ID and
click hereVideo by:
d
11fi)
a
show that question
look at solution
Question ID: 100130110060
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110060
Submit Yours! Copy Question ID and
click hereVideo by:
d
11fii)
a
$-1,3,4$
Question ID: 100130110070
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130110070
Submit Yours! Copy Question ID and
click hereVideo by:
d
12ai)
a
$\angle ACB=60^\circ$
Question ID: 100130120010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120010
Submit Yours! Copy Question ID and
click hereVideo by:
d
12aii)
a
$\angle ADX=30^\circ$
Question ID: 100130120020
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120020
Submit Yours! Copy Question ID and
click hereVideo by:
d
12aiii)
a
$\angle CAB=70^\circ$
Question ID: 100130120030
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120030
Submit Yours! Copy Question ID and
click hereVideo by:
d
12bi)
a
show that question
look at solution
Question ID: 100130120040
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120040
Submit Yours! Copy Question ID and
click hereVideo by:
d
12bii)
a
$\left(\frac{-a}{2},\frac{a}{16}\right)$
Question ID: 100130120050
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120050
Submit Yours! Copy Question ID and
click hereVideo by:
d
12ci)
a
show that question
look at solution
Question ID: 100130120060
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120060
Submit Yours! Copy Question ID and
click hereVideo by:
d
12cii)
a
$h\approx910$
Question ID: 100130120070
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120070
Submit Yours! Copy Question ID and
click hereVideo by:
d
12di)
a
show that question
look at solution
Question ID: 100130120080
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120080
Submit Yours! Copy Question ID and
click hereVideo by:
d
12dii)
a
show that question
look at solution
Question ID: 100130120090
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120090
Submit Yours! Copy Question ID and
click hereVideo by:
d
12diii)
a
$\approx2.57$
Question ID: 100130120100
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130120100
Submit Yours! Copy Question ID and
click hereVideo by:
d
13ai)
a
$x=3,7$
Question ID: 100130130010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130010
Submit Yours! Copy Question ID and
click hereVideo by:
d
13aii)
a
$\sqrt{11}$ms$^{-1}$
Question ID: 100130130020
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130020
Submit Yours! Copy Question ID and
click hereVideo by:
d
13aiii)
a
$a=2$, $c=5$, $n=\frac{\sqrt{11}}{2}$
Question ID: 100130130030
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130030
Submit Yours! Copy Question ID and
click hereVideo by:
d
13bi)
a
$a_2=\left(\begin{array}{cc} 18\\2\end{array}\right)\dfrac{2^{16}}{3^2}$
Question ID: 100130130040
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130040
Submit Yours! Copy Question ID and
click hereVideo by:
d
13bii)
a
$\left(\begin{array}{cc}18\\9\end{array}\right)\left(\dfrac23\right)^9$
Question ID: 100130130050
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130050
Submit Yours! Copy Question ID and
click hereVideo by:
d
13c)
a
proof question
look at solutions
Question ID: 100130130060
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130060
Submit Yours! Copy Question ID and
click hereVideo by:
d
13di)
a
proof question
look at solutions
Question ID: 100130130070
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130070
Submit Yours! Copy Question ID and
click hereVideo by:
d
13dii)
a
show that question
look at solution
Question ID: 100130130080
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130130080
Submit Yours! Copy Question ID and
click hereVideo by:
d
14ai)
a
show that question
look at solution
Question ID: 100130140010
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140010
Submit Yours! Copy Question ID and
click hereVideo by:
d
14aii)
a
$\frac{\pi}{6}$ below the horizontal
Question ID: 100130140020
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140020
Submit Yours! Copy Question ID and
click hereVideo by:
d
14aiii)
a
downwards, for explanation see solution
Question ID: 100130140030
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140030
Submit Yours! Copy Question ID and
click hereVideo by:
d
14bi)
a
show that question
look at solution
Question ID: 100130140040
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140040
Submit Yours! Copy Question ID and
click hereVideo by:
d
14bii)
a
$x=1-e^{-t}$
Question ID: 100130140050
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140050
Submit Yours! Copy Question ID and
click hereVideo by:
d
14biii)
a
$\lim_{t\to\infty}x=1$
Question ID: 100130140060
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
$\lim_{t\to\infty}x=1$
Question ID: 100130140060
Submit Yours! Copy Question ID and click here
Solution by: ada
Question ID: 100130140060
Submit Yours! Copy Question ID and
click hereVideo by:
d
14ci)
a
explain question
look at solution
Question ID: 100130140070
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140070
Submit Yours! Copy Question ID and
click hereVideo by:
d
14cii)
a
$\left(\begin{array}{cc}4\\4\end{array}\right)\left(\dfrac12\right)^5+\left(\begin{array}{cc}5\\4\end{array}\right)\left(\dfrac12\right)^6+\left(\begin{array}{cc}6\\4\end{array}\right)\left(\dfrac12\right)^7$
Question ID: 100130140080
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
$\left(\begin{array}{cc}4\\4\end{array}\right)\left(\dfrac12\right)^5+\left(\begin{array}{cc}5\\4\end{array}\right)\left(\dfrac12\right)^6+\left(\begin{array}{cc}6\\4\end{array}\right)\left(\dfrac12\right)^7$
Question ID: 100130140080
Submit Yours! Copy Question ID and click here
Solution by: ada
Question ID: 100130140080
Submit Yours! Copy Question ID and
click hereVideo by:
d
14ciii)
a
proof question
look at solution
Question ID: 100130140090
Submit Yours! Copy Question ID and
click hereQuestion by:
Answer by: ada
s
v
Question ID: 100130140090
Submit Yours! Copy Question ID and
click hereVideo by:
d
Answers
1) A
2) C
3) B
4) C
5) A
6) D
7) B
8) B
9) D
10) C
11a) $\frac12x-\frac14\sin2x+c$
11b) $\theta=\frac{\pi}{4}$ or $\theta=45^\circ$
11c) $-3 < x\le 1$
11d) $13\left(x+\tan^{-1}\left(\frac{12}{5}\right)\right)$
11e) $\frac14\left(\ln3+\frac23\right)$
11fi) show that question
look at solution
11fii) $-1,3,4$
12ai) $\angle ACB=60^\circ$
12aii) $\angle ADX=30^\circ$
12aiii) $\angle CAB=70^\circ$
12bi) show that question
look at solution
12bii) $\left(\frac{-a}{2},\frac{a}{16}\right)$
12ci) show that question
look at solution
12cii) $h\approx910$
12di) show that question
look at solution
12dii) show that question
look at solution
12diii) $\approx2.57$
13ai) $x=3,7$
13aii) $\sqrt{11}$ms$^{-1}$
13aiii) $a=2$, $c=5$, $n=\frac{\sqrt{11}}{2}$
13bi) $a_2=\left(\begin{array}{cc} 18\\2\end{array}\right)\dfrac{2^{16}}{3^2}$
13bii) $\left(\begin{array}{cc}18\\9\end{array}\right)\left(\dfrac23\right)^9$
13c) proof question
look at solutions
13di) proof question
look at solutions
13dii) show that question
look at solution
14ai) show that question
look at solution
14aii) $\frac{\pi}{6}$ below the horizontal
14aiii) downwards, for explanation see solution
14bi) show that question
look at solution
14bii) $x=1-e^{-t}$
14biii) $\lim_{t\to\infty}x=1$
14ci) explain question
look at solution
14cii) $\left(\begin{array}{cc}4\\4\end{array}\right)\left(\dfrac12\right)^5+\left(\begin{array}{cc}5\\4\end{array}\right)\left(\dfrac12\right)^6+\left(\begin{array}{cc}6\\4\end{array}\right)\left(\dfrac12\right)^7$
14ciii) proof question
look at solution
Solutions
1)
2)
3)
4) Choose $8$ students from $12$ so $^{12}C_8$
Choose $1$ student from $4$ so $^{4}C_1$
Both events happening so AND event so multiply $^{12}C_8$$\times ^4C_1$
5)
6)
7)
8)
9)
10)
11a)
11b)
11c)
11d)
11e)
11fi)
11fii)
12ai)
12aii)
12aiii)
12bi)
12bii)
12ci)
12cii)
12di)
12dii)
12diii)
13ai)
13aii)
13aiii)
13bi)
13bii)
13c)
13di)
13dii)
14ai)
14aii)
14aiii)
14bi)
14bii)
14biii) $\lim_{t\to\infty}x=1$
14ci)
14cii) $\left(\begin{array}{cc}4\\4\end{array}\right)\left(\dfrac12\right)^5+\left(\begin{array}{cc}5\\4\end{array}\right)\left(\dfrac12\right)^6+\left(\begin{array}{cc}6\\4\end{array}\right)\left(\dfrac12\right)^7$
14ciii)